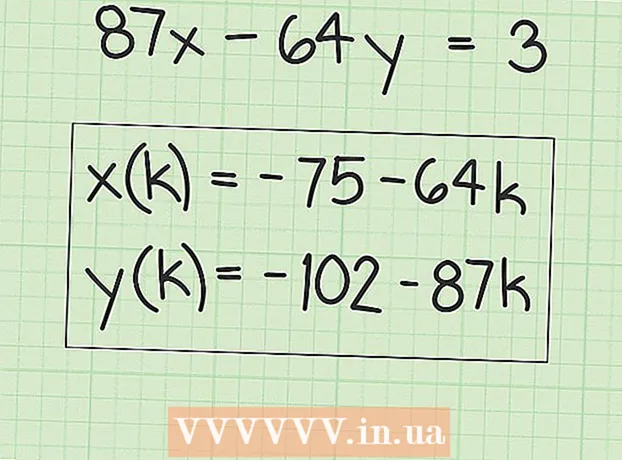
Мазмұны

• Қадамдар
• 4 -тің 1 -бөлігі: Теңдеуді қалай жазу керек
• 4 -тің 2 -бөлігі: Евклид алгоритмі қалай жазылады
• 4 -тің 3 -ші бөлімі: Евклид алгоритмін қолданып шешімді қалай табуға болады
• 4 -ші бөлімнің 4 -ші бөлігі: Шексіз басқа шешімдерді табыңыз

Сызықтық диофантикалық теңдеуді шешу үшін бүтін сандар болып табылатын «x» және «y» айнымалыларының мәндерін табу керек. Бүтін санды шешім әдеттегіден күрделірек және белгілі бір әрекеттер жиынтығын қажет етеді. Алдымен коэффициенттердің ең үлкен ортақ бөлгішін (GCD) есептеу керек, содан кейін шешімін табу керек. Сызықтық теңдеуге бір бүтін шешімді тапқан соң, басқа шешімдердің шексіз санын табу үшін қарапайым үлгіні қолдануға болады.

Қадамдар

4 -тің 1 -бөлігі: Теңдеуді қалай жазу керек

1. 1 Теңдеуді стандартты түрде жазыңыз. Сызықтық теңдеу - айнымалылардың көрсеткіштері 1 -ден аспайтын теңдеу. Мұндай сызықтық теңдеуді шешу үшін алдымен оны стандартты түрде жаз. Сызықтық теңдеудің стандартты формасы келесідей: ${ Displaystyle Ax + By = C}$, қайда ${ Displaystyle A, B}$ және ${ Displaystyle C}$ - бүтін сандар.
   • Егер теңдеу басқа түрде берілсе, оны негізгі алгебралық амалдарды қолдана отырып, стандартты күйге келтіріңіз. Мысалы, теңдеуді ескере отырып ${ Displaystyle 23x + 4y -7x = -3y + 15}$... Ұқсас терминдерді келтіріңіз және теңдеуді келесі түрде жазыңыз: ${ Displaystyle 16x + 7y = 15}$.
2. 2 Теңдеуді жеңілдетіңіз (мүмкін болса). Теңдеуді стандартты түрде жазғанда, коэффициенттерге қараңыз ${ Displaystyle A, B}$ және ${ Displaystyle C}$... Егер бұл коэффициенттерде GCD болса, барлық үш коэффициентті оған бөліңіз. Мұндай жеңілдетілген теңдеудің шешімі де бастапқы теңдеудің шешімі болады.
   • Мысалы, егер барлық үш коэффициент жұп болса, оларды кем дегенде 2 -ге бөліңіз. Мысалы:
     • ${ Displaystyle 42x + 36y = 48}$ (барлық мүшелер 2 -ге бөлінеді)
     • ${ Displaystyle 21x + 18y = 24}$ (қазір барлық мүшелер 3 -ке бөлінеді)
     • ${ Displaystyle 7x + 6y = 8}$ (бұл теңдеуді енді жеңілдетуге болмайды)
3. 3 Теңдеуді шешуге болатынын тексеріңіз. Кейбір жағдайларда теңдеудің шешімі жоқ екенін бірден айтуға болады. Егер «С» коэффициенті «А» және «В» коэффициенттерінің ГКД бойынша бөлінбесе, онда теңдеудің шешімдері болмайды.
   • Мысалы, егер екі коэффициент те ${ Displaystyle A}$ және ${ Displaystyle B}$ тең болады, онда коэффициент ${ Displaystyle C}$ жұп болуы керек. Бірақ егер ${ Displaystyle C}$ таңқаларлық, содан кейін шешім жоқ.
     • Теңдеу ${ Displaystyle 2x + 4y = 21}$ бүтін шешімдер жоқ.
     • Теңдеу ${ Displaystyle 5x + 10y = 17}$ бүтін шешімдер жоқ, өйткені теңдеудің сол жағы 5 -ке бөлінеді, ал оң жағы - жоқ.

4 -тің 2 -бөлігі: Евклид алгоритмі қалай жазылады

1. 1 Евклид алгоритмін түсінеді. Бұл қайталанатын бөлімдер тізбегі, онда алдыңғы қалдық келесі бөлгіш ретінде пайдаланылады. Сандарды интегралды түрде бөлетін соңғы бөлуші - екі санның ең үлкен ортақ бөлгіші (GCD).
   • Мысалы, Евклид алгоритмін қолдана отырып, 272 және 36 сандарының GCD табайық:
     • ${ Displaystyle 272 = 7 * 36 + 20}$ - үлкен санды (272) кішісіне (36) бөліп, қалғанына (20) назар аударыңыз;
     • ${ displaystyle 36 = 1 * 20 + 16}$ - алдыңғы бөлгішті (36) алдыңғы қалдыққа (20) бөлу. Жаңа қалдыққа назар аударыңыз (16);
     • ${ Displaystyle 20 = 1 * 16 + 4}$ - алдыңғы бөлгішті (20) алдыңғы қалдыққа (16) бөлу. Жаңа қалдыққа назар аударыңыз (4);
     • ${ displaystyle 16 = 4 * 4 + 0}$ - Алдыңғы бөлгішті (16) алдыңғы қалдыққа (4) бөліңіз. Қалған 0 болғандықтан, біз 4 - бұл 272 және 36 бастапқы екі санның GCD деп айта аламыз.
2. 2 Евклид алгоритмін «А» және «В» коэффициенттеріне қолданыңыз. Сызықтық теңдеуді стандартты түрде жазғанда, «А» және «В» коэффициенттерін анықтаңыз, содан кейін оларға GCD табу үшін Евклид алгоритмін қолданыңыз. Мысалы, сызықтық теңдеу берілген ${ Displaystyle 87x-64y = 3}$.
   • Міне, Евклидтің A = 87 және В = 64 коэффициенттерінің алгоритмі:
     • ${ displaystyle 87 = 1 * 64 + 23}$
     • ${ displaystyle 64 = 2 * 23 + 18}$
     • ${ displaystyle 23 = 1 * 18 + 5}$
     • ${ displaystyle 18 = 3 * 5 + 3}$
     • ${ displaystyle 5 = 1 * 3 + 2}$
     • ${ displaystyle 3 = 1 * 2 + 1}$
     • ${ displaystyle 2 = 2 * 1 + 0}$
3. 3 Ең үлкен ортақ факторды (GCD) табыңыз. Соңғы бөлгіш 1 болғандықтан, GCD 87 және 64 - 1. Осылайша, 87 мен 64 - бір -біріне қатысты жай сандар.
4. 4 Нәтижені талдаңыз. Gcd коэффициенттерін тапқанда ${ Displaystyle A}$ және ${ Displaystyle B}$, коэффициентімен салыстырыңыз ${ Displaystyle C}$ бастапқы теңдеу. Егер ${ Displaystyle C}$ gcd арқылы бөлінеді ${ Displaystyle A}$ және ${ Displaystyle B}$, теңдеудің бүтін сандық шешімі бар; әйтпесе теңдеудің шешімі болмайды.
   • Мысалы, теңдеу ${ Displaystyle 87x-64y = 3}$ шешуге болады, себебі 3 1 -ге бөлінеді (gcd = 1).
   • Мысалы, GCD = 5 делік. 3 5 -ке біркелкі бөлінбейді, сондықтан бұл теңдеуде бүтін шешімдер жоқ.
   • Төменде көрсетілгендей, егер теңдеуде бір бүтін шешім болса, онда басқа бүтін шешімдердің шексіз саны болады.

4 -тің 3 -ші бөлімі: Евклид алгоритмін қолданып шешімді қалай табуға болады

1. 1 GCD есептеуге арналған қадамдарды нөмірлеңіз. Сызықтық теңдеудің шешімін табу үшін ауыстыру мен жеңілдету процесінің негізі ретінде евклид алгоритмін қолдану қажет.
   • GCD есептеуге арналған қадамдарды нөмірлеуден бастаңыз. Есептеу процесі келесідей:
     • ${ displaystyle { text {1 -қадам}}: 87 = (1 * 64) +23}$
     • ${ displaystyle { text {2 -қадам}}: 64 = (2 * 23) +18}$
     • ${ displaystyle { text {3 -қадам}}: 23 = (1 * 18) +5}$
     • ${ displaystyle { text {4 -қадам}}: 18 = (3 * 5) +3}$
     • ${ displaystyle { text {5 -қадам}}: 5 = (1 * 3) +2}$
     • ${ displaystyle { text {6 -қадам}}: 3 = (1 * 2) +1}$
     • ${ displaystyle { text {7 -қадам}}: 2 = (2 * 1) +0}$
2. 2 Қалған бөлігі бар соңғы қадамға назар аударыңыз. Қалғанды ​​оқшаулау үшін осы қадамның теңдеуін қайта жазыңыз.
   • Біздің мысалда қалдығы бар соңғы қадам 6 -қадам болып табылады. Қалған 1 -қадам. 6 -қадамдағы теңдеуді келесі түрде қайта жазыңыз:
     • ${ Displaystyle 1 = 3- (1 * 2)}$
3. 3 Алдыңғы қадамның қалған бөлігін оқшаулаңыз. Бұл процесс біртіндеп «жоғары көтерілу» болып табылады. Алдыңғы қадамдағы теңдеудегі қалдықты оқшаулаған сайын.
   • 5 -қадамдағы теңдеудің қалған бөлігін оқшаулаңыз:
     • ${ Displaystyle 2 = 5- (1 * 3)}$ немесе ${ Displaystyle 2 = 5-3}$
4. 4 Ауыстырыңыз және жеңілдетіңіз. Назар аударыңыз, 6 -қадамдағы теңдеуде 2 саны бар, ал 5 -қадамдағы теңдеуде 2 саны оқшауланған. 6 -қадамдағы теңдеудегі «2» орнына 5 -қадамдағы өрнекті ауыстырыңыз:
   • ${ Displaystyle 1 = 3-2}$ (6 -қадамның теңдеуі)
   • ${ Displaystyle 1 = 3- (5-3)}$ (2 орнына өрнек ауыстырылды)
   • ${ Displaystyle 1 = 3-5 + 3}$ (ашық жақшалар)
   • ${ Displaystyle 1 = 2 (3) -5}$ (жеңілдетілген)
5. 5 Ауыстыру және жеңілдету процесін қайталаңыз. Евклид алгоритмі бойынша кері ретпен қозғалып, сипатталған процесті қайталаңыз. Әр жолы сіз алдыңғы қадамдағы теңдеуді қайта жазып, оны соңғы теңдеуге қосасыз.
   • Біз қарастырған соңғы қадам 5 -қадам болды. 4 -қадамға өтіңіз және қалған қадамды теңдеуде оқшаулаңыз:
     • ${ Displaystyle 3 = 18- (3 * 5)}$
   • Бұл өрнекті соңғы теңдеудегі «3» дегенге ауыстырыңыз:
     • ${ Displaystyle 1 = 2 (18-3 * 5) -5}$
     • ${ Displaystyle 1 = 2 (18) -6 (5) -5}$
     • ${ Displaystyle 1 = 2 (18) -7 (5)}$
6. 6 Ауыстыру және жеңілдету процесін жалғастырыңыз. Бұл процесс сіз Евклид алгоритмінің бастапқы сатысына жеткенше қайталанады. Процестің мақсаты - шешілетін бастапқы теңдеудің 87 және 64 коэффициенттері бар теңдеуді жазу. Біздің мысалда:
   • ${ Displaystyle 1 = 2 (18) -7 (5)}$
   • ${ Displaystyle 1 = 2 (18) -7 (23-18)}$ (3 -қадамдағы өрнекті ауыстырды)
     • ${ Displaystyle 1 = 2 (18) -7 (23) +7 (18)}$
     • ${ Displaystyle 1 = 9 (18) -7 (23)}$
   • ${ Displaystyle 1 = 9 (64-2 * 23) -7 (23)}$ (өрнекті 2 -қадамнан алмастырды)
     • ${ Displaystyle 1 = 9 (64) -18 (23) -7 (23)}$
     • ${ Displaystyle 1 = 9 (64) -25 (23)}$
   • ${ Displaystyle 1 = 9 (64) -25 (87-64)}$ (1 -қадамдағы өрнекті ауыстырды)
     • ${ Displaystyle 1 = 9 (64) -25 (87) +25 (64)}$
     • ${ Displaystyle 1 = 34 (64) -25 (87)}$
7. 7 Алынған теңдеуді бастапқы коэффициенттерге сәйкес қайта жазыңыз. Евклид алгоритмінің бірінші сатысына оралғанда, алынған теңдеуде бастапқы теңдеудің екі коэффициенті бар екенін көресіз. Теңдеуді оның мүшелерінің реті бастапқы теңдеудің коэффициенттеріне сәйкес келетін етіп қайта жазыңыз.
   • Біздің мысалда бастапқы теңдеу ${ Displaystyle 87x-64y = 3}$... Сондықтан алынған теңдеуді қайта жазыңыз, сонда коэффициенттер біркелкі болады.«64» коэффициентіне ерекше назар аударыңыз. Бастапқы теңдеуде бұл коэффициент теріс, ал евклид алгоритмінде оң болады. Демек, 34 факторды теріс ету керек. Соңғы теңдеу келесі түрде жазылады:
     • ${ Displaystyle 87 (-25) -64 (-34) = 1}$
8. 8 Шешімді табу үшін сәйкес мультипликаторды қолданыңыз. Назар аударыңыз, біздің мысалда GCD = 1, сондықтан соңғы теңдеу 1-ге тең. Бірақ бастапқы теңдеу (87x-64y) 3-ке тең. Сондықтан шешімін алу үшін соңғы теңдеудегі барлық мүшелерді 3-ке көбейту керек:
   • ${ Displaystyle 87 (-25 * 3) -64 (-34 * 3) = 1 * 3}$
   • ${ Displaystyle 87 (-75) -64 (-102) = 3}$
9. 9 Бүтін санды шешуді теңдеуге жаз. Бастапқы теңдеудің коэффициенттеріне көбейтілетін сандар - бұл теңдеудің шешімдері.
   • Біздің мысалда шешімді жұп координаталар түрінде жазыңыз: ${ Displaystyle (x, y) = ( - 75, -102)}$.

4 -ші бөлімнің 4 -ші бөлігі: Шексіз басқа шешімдерді табыңыз

1. 1 Шешімдердің шексіз саны бар екенін түсініңіз. Егер сызықтық теңдеудің бір бүтін шешімі болса, онда оның шексіз көп бүтін шешімдері болуы керек. Міне жылдам дәлел (алгебралық түрде):
   • ${ Displaystyle Ax + By = C}$
   • ${ Displaystyle A (x + B) + B (y-A) = C}$ (егер сіз «В» -ді «x» -ке қосып, «y» -ден «A» -ды алып тастасаңыз, онда бастапқы теңдеудің мәні өзгермейді)
2. 2 Бастапқы x және y мәндерін жазыңыз. Келесі (шексіз) шешімдерді есептеу үлгісі сіз тапқан жалғыз шешімнен басталады.
   • Біздің мысалда шешім координаттар жұбы болып табылады ${ Displaystyle (x, y) = ( - 75, -102)}$.
3. 3 «B» коэффициентін «x» мәніне қосыңыз. Жаңа x мәнін табу үшін мұны жасаңыз.
   • Біздің мысалда x = -75 және B = -64:
     • ${ Displaystyle x = -75 + ( - 64) = - 139}$
   • Осылайша, жаңа «x» мәні: x = -139.
4. 4 «Y» мәнінен «А» коэффициентін алып тастаңыз. Бастапқы теңдеудің мәні өзгермеуі үшін, «x» -ке бір санды қосқанда, «y» -ден басқа санды алып тастау керек.
   • Біздің мысалда y = -102 және A = 87:
     • ${ Displaystyle y = -102-87 = -189}$
   • Осылайша, «y» үшін жаңа мән: y = -189.
   • Жаңа координаттар жұбы келесідей жазылады: ${ Displaystyle (x, y) = ( - 139, -189)}$.
5. 5 Шешімді тексеріңіз. Жаңа координаталар жұбы бастапқы теңдеудің шешімі екенін тексеру үшін мәндерді теңдеуге қосыңыз.
   • ${ Displaystyle 87x-64y = 3}$
   • ${ Displaystyle 87 (-139) -64 (-189) = 3}$
   • ${ Displaystyle 3 = 3}$
   • Теңдік сақталғандықтан, шешім дұрыс.
6. 6 Көптеген шешімдерді табу үшін өрнектерді жазыңыз. «X» мәндері бастапқы шешімге және «В» факторының кез келген еселігіне тең болады. Бұл келесі өрнек түрінде жазылуы мүмкін:
   • x (k) = x + k (B), мұнда «x (k)» - «x» мәндерінің жиынтығы, ал «x» - сіз тапқан «x» бастапқы (бірінші) мәні.
     • Біздің мысалда:
     • ${ Displaystyle x (k) = - 75-64k}$
   • y (k) = y-k (A), мұнда y (k)-у мәндерінің жиынтығы, ал у-сіз тапқан бастапқы (бірінші) у мәні.
     • Біздің мысалда:
     • ${ Displaystyle y (k) = - 102-87k}$